머신 러닝으로 금 시세를 예측 해보자 - 모델 평가&활용

1. 모델 검증 방법

2. 모델 검증 & 개선

3. 모델 활용 시뮬레이션 & 개선

 

과거의 포스팅에서 ARIMA, Prophet, LSTM의 간단한 설명과 모델 구축의 기본에 대해서 알아봤다.

본 포스팅에서는 모델의 평가와 활용법에 대해 알아보도록 하겠다.

 

결론부터 말하면,  LSTM 모델을 사용하여 2015년 10월부터 현재까지(2020년 4월 23일) 금을 투자하였다면,  221%의 수익률(2015년부터 안 팔고 보유했을 경우의 수익률 153%)을 올렸을 것으로 나타난다.

 

 

1. 모델 검증 방법

먼저 모델의 검증 방법으로는 one-step forecast방법을 사용하였다.

시계열 데이터는 일반적 cross validation 방법으로는  검증이 불가능하다. 이는 일반적인 데이터와 다르게 시계열 데이터에는 순서가 존재하기 때문이다.

일반적인 cross validation방법               (출처) https://scikit-learn.org/stable/modules/cross_validation.html

 

 

one-step forecast validation은 하기와 같이 시간이 지남에 따라 매일매일 업데이트되는 데이터 (밑의 그림의 파란 점)로 모델을 업데이트하고 그다음 날(밑의 그림의 빨간 점)을 예측하는 프로세스를 반복하는 방법이다. 

one-step forecast validation 방법      (출처) https://otexts.com/fpp3/tscv.html

2000.01.01~2015.07.27의 데이터로 모델을 사전 학습시키고, 2015.07.28 ~2020.04.23까지의 데이터를 위의 one-step forecast 방법으로 예측을 해 보겠다. 즉, 2015.10.02의 데이터를 예측하기 전에는 기존에 학습된 모델에 2015.10.01의 데이터를 업데이트하고 2015.10.02의 데이터를 예측하고, 그 2015.10.03의 예측은 2015.10.02까지의 데이터를 업데이트 후에 하는 방식이다.

금 시세 그래프, 파란색 영역-모델 사전 학습 영역, 빨간색 영역 - 모델 예측 검증 영역

 

모델을 비교하는 값으로는 먼저  평균 제곱 오차(Mean-square-error)를 기준으로 하겠다.

평균 제곱 오차

 

2. 모델 검증 & 개선

 

필요한 패키지를 불러온다. ARIMA모델은 계절 정의 요인도 분석이 가능한 SARIMA모델을, Prophet은 fbprophet의 모델을  LSTM은 텐서 플로우의 패키지의 모델을 사용하였다.

import warnings
warnings.filterwarnings("ignore")

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import datetime

from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split

from statsmodels.tsa.statespace.sarimax import SARIMAX

from fbprophet import Prophet

import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense, LSTM, Bidirectional, Dropout, TimeDistributed
from tensorflow.keras.preprocessing.sequence import pad_sequences
from tensorflow.keras.optimizers import *
from tensorflow.keras.models import load_model

LSTM 모델 구축과 LSTM모델용 데이터 분리 함수를 정의한다.

def step_split(x_sequence, y_sequence, n_steps, n_features, n_forwards, n_predict_steps, test_set=False):
  x_sequence = np.array(x_sequence).reshape(-1, n_features)
  y_sequence = np.array(y_sequence).reshape(-1, 1)

  X, y = list(), list()
  if test_set:
    X = x_sequence[-n_steps:]
    X = np.array(X)
    X = X.reshape(1, n_steps, n_features)
  else:
    end = len(x_sequence) - n_steps - n_forwards - n_predict_steps + 2
    for i in range(end):
      seq_x = x_sequence[i:i+n_steps]
      seq_y = y_sequence[i+n_steps+n_forwards-1:i+n_steps+n_forwards+n_predict_steps-1]
      X.append(seq_x)
      y.append(seq_y)
    X = np.array(X)
    y = np.array(y)
    X = X.reshape(X.shape[0], n_steps, n_features)
    y = y.reshape(y.shape[0], n_predict_steps)

  return X, y


def create_model(stateful,batch_size, n_steps, n_features):
    model = Sequential()
    model.add(LSTM(32,
                batch_input_shape=(batch_size, n_steps, n_features),
                stateful=stateful))
    model.add(Dense(1))
    optimizer = Adam()
    model.compile(loss='mse', optimizer=optimizer)
    return model

 

모델 학습&예측 데이터는 2000년부터의 일별 금 시세이다.

 

각 모델을 정의하고 예측을 진행하였다.

#금 시세 데이터 불러오기
gold_df = pd.read_csv('gold_price.csv')

# 2000년 부터의 데이터만 사용
X = gold_df[gold_df.index >= datetime.datetime(2000,1,1)]
y = gold_df[gold_df.index >= datetime.datetime(2000,1,1)]


#LSTM의 학습과 예측 기간 설정
n_steps = 32
training_period = 512 + n_steps
n_features = 1
n_forwards = 1
n_predict_steps = 1

#테스트 기간 설정
end = len(X) - n_steps - training_period
validation_size = 1200
start = end - validation_size





#예측 결과를 담을 리스트 만들기
yhat_arima_list = list()
yhat_prophet_list = list()
yhat_logistic_prophet_list = list()
yhat_lstm_list = list()
y_real_list = list()
predict_index_list = list()

#LSTM의 학습 파라미터 설정
stateful = True
batch_size = 1
epochs = 1


#LSTM모델의 사전 학습
lstm_model = create_model(stateful,batch_size,n_steps,n_features)
data_x = X[start-training_period:start].values.reshape(-1, n_features)
data_y = y[start-training_period:start].values.reshape(-1, 1)
scaler = MinMaxScaler(feature_range=(-1,1))
scaler.fit(data_x)
data_x = scaler.transform(data_x)
data_y = scaler.transform(data_y)
x_train, y_train = step_split(data_x, data_y, n_steps,n_features, n_forwards, n_predict_steps)


pretrain_epoch = 60
for j in range(pretrain_epoch): 
  print(f'Epoch {j + 1}/{pretrain_epoch}')
  lstm_model.fit(x_train, y_train,
                    batch_size=batch_size,
                    epochs=1,
                    verbose=2,
                    shuffle=False,
                    validation_split=0.1
                      )
  lstm_model.reset_states()



#one-step time series forecast시작
for i in tqdm_notebook(range(start, end)):
  # 학습은 과거 전 구간이 아닌 예측날 기준 512일 이전의 데이터만 학습하도록 하겠다.
  data = X[i:i+training_period+n_steps]
  y_real = X.values[i+training_period+n_steps].item()
  y_real_list.append(y_real)
  predict_index = X.index[i+training_period+n_steps].date()
  predict_index_list.append(predict_index)


  #SARIMA모델 정의와 학습
  sarima_model = SARIMAX(data.values, order=(0,1,1), seasonal_order=(0, 1, 1, 12), trend='c', enforce_stationarity=False, enforce_invertibility=False)
  model_fit = sarima_model.fit()
  sarima_forecast = model_fit.forecast(1).item()
  yhat_arima_list.append(sarima_forecast)
  
  #Prophet모델 정의와 학습
  prophet_model = Prophet(daily_seasonality = False)
  prophet_series = pd.DataFrame([data.index, data['gold_price']]).T
  prophet_series.columns = ['ds','y']
  prophet_model.fit(prophet_series)
  future =  prophet_model.make_future_dataframe(periods=1)
  prophet_forecast = prophet_model.predict(future[-1:])['yhat'].item()
  yhat_prophet_list.append(prophet_forecast)  


  #LSTM모델용 데이터 전처리 
  data_x = data.values.reshape(-1, n_features)
  data_y = data.values.reshape(-1, 1)


  scaler = MinMaxScaler(feature_range=(-1,1))
  scaler.fit(data_x)
  
  data_x = scaler.transform(data_x)
  data_y = scaler.transform(data_y)
  

  x_train, y_train = step_split(data_x, data_y, n_steps,n_features, n_forwards, n_predict_steps)
  x_test, _ = step_split(data_x, data_y, n_steps,n_features, n_forwards, n_predict_steps, True)
  
  #LSTM 모델 예측 실시
  lstm_model.fit(x_train, y_train,
                    batch_size=batch_size,
                    epochs=1,
                    verbose=0,
                    shuffle=False
                      )
  lstm_model.reset_states()
  lstm_forecast = scaler.inverse_transform(lstm_model.predict(x_test, batch_size=batch_size)).item()
  yhat_lstm_list.append(lstm_forecast)

결과를 그래프로 확인해 보면, Prophet을 제외하고는 얼추 예측이 가능한 것으로 보인다.

 특히 SARIMA 모델의 경우 완벽하게 예측하는 것으로 보인다. 하지만 전의 포스팅의 결과와 같이 그래프를 확대해서 확인해 보면, 단순히 전날의 값을 대부분 다음날의 예측 결과로 사용하는 것을 알 수 있다.

 

Prophet은 모델의 알고리즘의 구조상(일정 구간의 선형 예측+주기성+계절성) 단기 예측에는 적합하지 않으며, 중장기 예측에 적합한 것으로 보인다. Prophet에서 설계한 사용법은 아니지만, 데이터의 상한 하한을 그날의 값의 ±10% 이상은 변동하지 않는 제한을 두어 재학습을 해 보도록 하겠다.

for i in tqdm_notebook(range(start, end)):
  data = X[i:i+training_period+n_steps]

  prophet_series = pd.DataFrame([data.index, data['gold_price']]).T
  prophet_series.columns = ['ds','y']
  prophet_model = Prophet(growth = 'logistic', daily_seasonality = False)
  prophet_series['cap'] = prophet_series['y'].shift() * 1.1
  prophet_series['floor'] = prophet_series['y'].shift() * 0.9
  prophet_series.fillna(method='bfill', inplace=True)

  prophet_model.fit(prophet_series)
  future =  prophet_model.make_future_dataframe(periods=1)
  future['cap'] = prophet_series['cap'].append(pd.Series(prophet_series['y'].values[-1]*1.1),ignore_index=True)
  future['floor'] = prophet_series['floor'].append(pd.Series(prophet_series['y'].values[-1]*0.9),ignore_index=True)
  future.fillna(method='bfill', inplace=True)


  prophet_forecast = prophet_model.predict(future[-1:])['yhat'].item()
  yhat_logistic_prophet_list.append(prophet_forecast)  

재 학습의 결과 Prophet의 단기 예측 성능이 향상 된 것을 확인할 수 있다.

 

이제 MSE의 값으로 모델의 성능을 확인해 보자.

result_df = pd.DataFrame(list(zip(y_real_list, yhat_arima_list,yhat_prophet_list,yhat_logistic_prophet_list,yhat_lstm_list)),columns=['y','arima','prophet','prophet_logistic','lstm'],index=predict_index_list)
col_list = ['arima', 'prophet','prophet_logistic','lstm']
for col in col_list:
  mse = mean_squared_error(result_df['y'], result_df[col])
  print(f'{col} error: {mse}')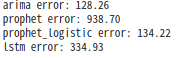

 

MSE의 값을 기준으로는 SARIMA, Prophet개선, LSTM, Prophet 의 예측 결과가 가장 신뢰성이 있는 것으로 나타났다.

 

하지만 단순히 MSE의 값을 가지고 이 모델이 실투자에 사용이 가능한지 아닌지는 판단이 힘들다. 다음장에서 모델을 실제 투자에 적용하였을 경우 어떠한 결과가 나오는지 시뮬레이션을 해 보도록 하겠다.

3. 모델의 활용 & 개선

 비현실적이긴 하지만 시뮬레이션에 앞서 몇가지 가정을 두도록 하겠다.

  1. 금의 매매와 매수의 값은 일치한다.

  2. 거래일의 매매, 매수 가격은 그 거래일의 종가로 일정하다.

  3. 금 매매, 매수의 수수료는 0원이다.

 

 투자 할때 현재의 가격은 중요하지 않다. 지금 금 값이 1000만 원/g이라고 투자를 하지 않고, 1만 원/g이라고 투자를 하는 것은 아니다. 우리는 투자하는 물건이 미래에 오를 것이냐 내릴 것이냐와 그 움직이는 비율은 어느 정도일 것이냐를 예측해서 투자를 결정한다. 즉 모델에서 예측한 미래(여기서는 내일)의 금 시세가 오늘의 시세보다 높으면 투자를 할 것이고 낮거나 같으면, 투자를 하지 않을 것이다.

 2015년 7월 28일 부터 약 5년간 모델을 사용하여 투자를 진행했다고 가정해 보자. 우리는 모델이 다음날 오른다고 하면 금을 사고 내리거나 변동이 없다고 하면, 금을 사지 않는다. 또한 만약 금을 살 결우 금 시세가 올랐는지 내렸는지 여부와 상관없이 다음날을 금을 판다고 가정하자.

 

result_df = pd.DataFrame(list(zip(y_real_list, yhat_arima_list,yhat_prophet_list,yhat_logistic_prophet_list,yhat_lstm_list)),columns=['y','arima','prophet','prophet_logistic','lstm'],index=predict_index_list)
result_df['ratio'] = result_df['y'].diff() / result_df['y'].shift()
result_df['y_shifted'] = result_df['y'].shift()
result_df['arima_direction'] = result_df.apply(lambda x: 1 if (x['arima'] - x['y_shifted']) > 0 else 0, axis=1) 
result_df['prophet_direction'] = result_df.apply(lambda x: 1 if (x['prophet'] - x['y_shifted']) > 0 else 0, axis=1) 
result_df['prophet_logistic_direction'] = result_df.apply(lambda x: 1 if (x['prophet_logistic'] - x['y_shifted']) > 0 else 0, axis=1) 
result_df['lstm_direction'] = result_df.apply(lambda x: 1 if (x['lstm'] - x['y_shifted']) > 0 else 0, axis=1) 

result_df['arima_simulation'] = result_df['y'][0]
result_df['prophet_simulation'] = result_df['y'][0]
result_df['prophet_logistic_simulation'] = result_df['y'][0]
result_df['lstm_simulation'] = result_df['y'][0]

for i in range(1,len(result_df)):
  result_df['arima_simulation'][i] = result_df['arima_simulation'][i-1] *(1 + result_df['arima_direction'][i]*result_df['ratio'][i])
  result_df['prophet_simulation'][i] = result_df['prophet_simulation'][i-1] *(1 + result_df['prophet_direction'][i]*result_df['ratio'][i])
  result_df['prophet_logistic_simulation'][i] = result_df['prophet_logistic_simulation'][i-1] *(1 + result_df['prophet_logistic_direction'][i]*result_df['ratio'][i])
  result_df['lstm_simulation'][i] = result_df['lstm_simulation'][i-1] *(1 + result_df['lstm_direction'][i]*result_df['ratio'][i])

plt.plot(result_df['y'], label='real_price', color='b')
plt.plot(result_df['arima_simulation'], label='SARIMA',color='r')
plt.plot(result_df['prophet_simulation'], label='Prophet',color='g')
plt.plot(result_df['prophet_logistic_simulation'], label='Prophet_modify',color='yellow')
plt.plot(result_df['lstm_simulation'], label='LSTM',color='grey')
plt.legend()
plt.show()

모든 모델이 그냥 2015년 7월 28일부터 금을 사서 보유하고 있었을 경우보다 수익률이 낮은 것을 볼 수 있다.

각 모델별 시뮬레이션 결과

하지만 우리는 여기서 모델을 개선할 방법을 찾을 수 있다. 현재의 모델들은 다음 날의 값을 예측 하지만, 우리가 필요한 정보는 단순히 미래에 오를 것인지 내릴 것인지의 여부이다.  LSTM으로 다음날 오를 것인지 내릴 것인지만을 판단하는 Binary Classification 모델을 구축하여 시뮬레이션을 다시 해 보도록 하겠다.

 

one-step forecast validation 의 정확도(accuracy)는 약 57%의 수준으로 나왔다. 물론 상승 하강의 어느 시기에 모델이 맞췄는지가 중요하긴 하지만, 일단 50% 이상의 정확도를 가지는 것은 좋은 결과를 예상할 수 있다.

Binary Classification LSTM의 정확도 변화 그래프

binary classification LSTM을 사용하면, 약 5년간 303%의 높은 수익률(금을 사서 그냥 두었을시의 수익률 158%)을 달성할 수 있는 결과가 나온다.

Binary Classfication LSTM의 금 투자 시뮬레이션 결과

 금 투자 방법과 여러가지 비현실적인 가정을 두었지만, 이러한 어프로치로 금 시세의 장기 예측, 주가, 유가의 장단기 예측 모델을 구축하면 투자의 판단의 좋은 재료로 활용할 수 있을 것이다.